Management
The Analytic Hierarchy Process (AHP) is an effective, multi-criteria decision-making method that helps you to assign logical, concrete values to your choices so you can make more informed judgments. Learn how to use AHP to intelligently structure and analyze complex problems and more easily synthesize your data with your criteria.
Key Concept
Named for a Greek oracle, the Delphi method is a technique for getting a consensus among experts in a given field (e.g., project management or recruitment) to participate anonymously in a panel and answer a few rounds of questionnaires. The facilitator solicits proposals (e.g., decision criteria) using a questionnaire and then summarizes the anonymous answers and circulates them back to the experts for comment or change. Typically, after two or three such rounds, the range of answers decreases and a consensus is reached that provides input into AHP’s decision-making process. One advantage is that the Delphi method reduces any overt influence from the opinions of other participants that are common in face-to-face meetings. If there are several decision makers, it’s advisable to use the Delphi method to define the criteria set.
A typical SAP customer project can be extremely complex, with high susceptibility to change, many stakeholders to manage, a variety of interrelationships with other ongoing projects, risks that are difficult to identify, and an inexact or shifting definition of scope. Decision makers must resolve numerous problems while satisfying multiple criteria, whether they are selecting an SAP project manager, a new technological solution, or a time-compression strategy. Such decisions — made in an increasingly complicated and rapidly changing business environment and potentially resulting in huge consequences — are too often founded on a haphazard, inexact combination of experience, logic, and inarticulate feelings. Unfortunately, while decision making necessarily tops the list of requisite management skills, few project managers have any actual training in it.
You can fill this gap using AHP. Thomas L. Saaty (an American mathematician at the University of Pittsburgh) first introduced this powerful and flexible method in the 1970s. Since then, the method has extended to the business realm in areas such as quality management, supplier selection, transportation route selection, human capital management, resource allocation, and forecasting. In fact, a number of prominent companies and organizations, such as NASA, General Motors, IBM, AOL, Hewlett-Packard, BP, Shell, Boeing, and NATO, have adopted it as an important tool.
I begin by explaining some basic AHP concepts: building a decision problem hierarchy, making pairwise comparisons, and analyzing sensitivity to change. (Decision problems are questions with a yes-or-no answer, depending on some input parameter.) Then, I show how AHP works on a sample project-management decision problem: selecting an SAP project manager. Finally, I explore several typical decision problems that occur during SAP implementations and provide sample decision hierarchies for them. After reading this article, you should be able to use AHP to intelligently structure and analyze complex problems, more easily synthesize your data with your criteria, and so lay a solid, rational foundation for making decisions in real-world situations.
Prerequisites
You need to have a basic knowledge about SAP project management. Also, if you first read the article, “Reduce project risk by integrating Project Management Body of Knowledge (PMBOK) tools and techniques with ASAP”, which was posted to the SAP Professional Journal knowledgebase in September/October 2005, you may find it easier to understand project problems.
Although AHP has mathematics behind it, you don’t need to worry about the math; you won’t have to solve any equations. A number of decision-support software tools are available that have been designed specifically to perform the necessary equations for AHP (e.g., ExpertChoice, DecisionLens, AHPproject, and Criterium DecisionPlus). For this article, I used AHPproject (www.AHPproject.com), which is free, Web-based decision-support software.
The Basics of AHP
AHP begins by taking a commonsense approach to analyzing decision-making problems. For a simple example, suppose you want to organize a working lunch so that new team members can get to know each other better and begin to exchange ideas. How do you choose a suitable restaurant? In your mind, you have some basic criteria: It needs to be reasonably close to the office, have good food and a good atmosphere, and stay within your allotted budget. So, you jot down a list of the restaurants nearby, ticking off the possible choices and crossing out the unsuitable ones. This decision process, then, involves three basic elements:
- The goal you want to achieve
- The criteria you must satisfy to successfully accomplish the goal
- The available options among which you must choose
People make decisions like this every day with scarcely a second thought. However, to make well-informed decisions in today’s highly differentiated, changing, and complex business environment, you need a method sophisticated enough to facilitate handling multiple factors, but simple enough to understand and actually use. This is particularly true when you need to consider not only readily quantifiable tangible factors (e.g., profit and loss), but also intangible ones (e.g., creative leadership), which are much harder to quantify. AHP provides the methodology and the metrics — applicable to tangibles and intangibles alike — to make intricate decision problems manageable.
In other words, as a multi-criteria decision-making methodology, AHP is designed specifically to handle structure complexity. The method arranges the composite elements of the basic “goal + criteria + alternatives” decision structure into hierarchical levels (Figure 1) and then applies a sound mathematical model to the hierarchy to generate the metrics used in the evaluative process.
You can expand a decision hierarchy to any degree of complexity according to your needs. With dedicated AHP software available, you can rationally organize complex decision problems, such as SAP projects, thereby greatly simplifying them. In addition, the AHP software makes it easy to change or rearrange the elements in the hierarchy to incorporate new information or developments. You can even alter the elements in a hierarchy to examine possible outcome variations, adding tremendous flexibility and adaptability to your decision-making process.

Figure 1
Model of a simple decision hierarchy
Applying AHP is a four-stage process, as shown in the following:
- AHP breaks down or decomposes the decision problem into a hierarchy of levels: level 1 is the goal; level 2 contains the criteria; intermediate levels represent sub-criteria (if needed); and the lowest level of the hierarchy (in this case, level 3) includes the alternatives.
- AHP analyzes the elements on each specific level of the hierarchy by comparing them with each other in a series of pairings (called pairwise or horizontal comparisons).
- As a result of the pairwise comparisons, AHP assigns a numerical value to each element. These numerical values, weighted in the context of the overall decision hierarchy, provide the mathematical matrix for the decision.
- AHP compares the various alternatives to one another, regarding each of the various criteria, to derive their relative weights and, thus, priorities. AHP performs a mathematical aggregation to derive the numerical priorities assigned to each alternative. You might consider this to be the vertical dimension of comparison.
Using the example of choosing a restaurant for a working lunch, let’s walk through the four-stage process to see how AHP works in practice. Once you understand AHP’s principal concepts, including how the basic mathematic model works and how to design the hierarchy, you’ll be ready to take on a real SAP project management problem (see the sidebar “Hierarchy Design”).
Sidebar: Hierarchy Design
Designing the problem hierarchy is more art than science; there are no strict rules for structuring the components of the problem. In fact, different decision makers may have different visions of the same problem, so it’s good practice to seek the input of others (such as stakeholders and experts) to make sure that you cover all of the key elements and organize them in the best way. One big payoff that comes from thinking through the process while you construct the hierarchy is a deeper understanding of the problem; the problem hierarchy helps you to understand all of the problem’s elements and to recognize the relationships among them.
Knowing the connections among all of the problem’s elements is especially helpful when you have to make further divisions into sub-criteria (and sub-sub-criteria and so on) — that is, when you need to decompose a complex decision problem into more manageable sub-problems. Decomposing often leads you to examine the problem to an unexpected depth. This may be especially true for understanding the so-called "intangibles". In the example, for instance, decomposing the rather vague criterion of “good atmosphere” should prompt you to ask what, precisely, “good” means: Not too crowded or noisy? Adequate table space? The availability of a conference room with Wi-Fi? Similarly, if your criteria for choosing a project manager include creativity or dynamic leadership, you may find that decomposing these qualities into more specific sub-criteria helps you to identify the particular elements most necessary for making your decision.
The Decision Problem Decomposed
The essential mathematical structure of a decision hierarchy is quite easy to understand. (The math becomes unwieldy only when it works on a complex problem, but the AHP software makes this easy to handle.) Returning to the lunch example, first identify the goal: to choose a suitable restaurant for a working lunch. AHP assigns a numerical value of 1.00 to the goal (some software products assign a value of 100.00, but the idea is the same). This makes sense because the goal constitutes the whole, while the various criteria and sub-criteria are the parts that contribute to the whole. So, if all the primary criteria in your decision hierarchy were equally weighted, the structure would look like the one in Figure 2.

Figure 2
Decision hierarchy with equally distributed mathematical weights
Being equally weighted, each one of the four criteria makes up one quarter of the whole; that is, each is 0.25 of 1.0. For example, suppose that the third criterion, atmosphere, has two sub-criteria. They are weighted at 0.125 each because they add up to the total value (0.25) of that particular criterion. Similarly, the fourth criterion, cuisine, has four sub-criteria, which add up to the total weight of that criterion (4 × 0.0625 = 0.25). You can expand this structure to any depth you want.
Analyzing the Elements
Criteria in real-world decisions are never equally weighted, so how do you arrive at their comparative values? Here again, AHP takes a commonsense approach. T.L. Saaty observed that people find it difficult to assign values in an absolute sense and that the attempt to do so actually increases the tendency to make more arbitrary valuations. Alternatively, it seems much more natural — and ultimately more reasonable — to make judgments and assign values by comparing the alternatives with one another. For example, look at the four main criteria: Any attempt to simply and unmethodically assign absolute values to cost, distance, environment, or type of cuisine amounts to little more than a guess and therefore, is more or less arbitrary. AHP, by contrast, advocates a systematic process of pairwise comparisons in which each element on one level of the hierarchy is compared to every other element on the same level to arrive at its relative value.
Note
Several enhancements for AHP are available to support group decision making. Daniel Saaty (not to be confused with Thomas L. Saaty) proposed a simple framework for analyzing a problem in a group, described in the sidebar “AHP Tips” below. More sophisticated methods use the weighted geometric mean or other mathematical tools, such as various aggregation procedures.
Sidebar: AHP Tips
The following advice may be helpful when you use AHP:
When defining the decision hierarchy for project problems, seek the input of senior managers about what criteria to use (especially when decisions relate to the company strategy).
If possible, invite experts to discuss comparisons — the problems are usually of an interdisciplinary nature, and sometimes professionals with dedicated knowledge may improve both the process and understanding of the results.
If you are analyzing a problem in a group and want to reach a consensus for a decision, administer this three-part test (proposed by Daniel Saaty) to all participants:
If someone answers no to any of these questions, he or she will be asked to communicate the reason for the disagreement and propose a solution. Remember that consensus merely reflects a choice with which you can live and support when you leave today. It’s not necessarily your preferred choice.
Comparative judgments begin with a verbal scale that enables decision makers to incorporate their knowledge, experience, and intuition in a simple and natural way. (AHP translates this verbal scale into more precise mathematical terms.) Asking whether cost or atmosphere is more important, for instance, gives you something concrete with which to work. Even though you must adhere to a budget limit, a good working environment for the lunch is more important in the overall scheme of things — in fact, you might verbally say that it’s “much more important.” AHP then translates the verbal judgments into a simple scale of whole numbers (Table 1).
|
1
|
Indifferent (equally preferred) |
|
3
|
Weak preference (moderately preferred) |
|
5
|
Preference (strongly preferred) |
|
7
|
Strong preference (very strongly preferred) |
|
9
|
Very strong preference (extremely preferred) |
|
2, 4, 6, 8
|
Intermediate values available if needed |
|
| Table 1 |
The verbal Saaty scale (proposed by T.L. Saaty) |
Assign a Numerical Value
With this scale in mind, you then set up a matrix with an equal number of rows and columns according to the number of elements you plan to compare. You compare each row element against the elements in the columns for its dominance over those elements and assign the corresponding numerical value. So, for instance, the number 5 in the atmosphere row shows that this criterion is “strongly preferred” over the cost criterion; the number 3 in the cuisine row shows that this criterion is “moderately preferred” to cost; and so on (Table 2). Conversely, if you look at the cost row, you find reciprocal fractions for atmosphere (1/5) and cuisine (1/3); that is, if atmosphere is five times as important as cost, then cost must be one-fifth as important as atmosphere. Notice also that whenever an element is compared to itself, it is assigned a value of 1, “equally preferred.”
| Cost |
1
|
3
|
1/5
|
1/3
|
| Distance |
1/3
|
1
|
1/7
|
1/5
|
| Atmosphere |
5
|
7
|
1
|
3
|
| Cuisine |
3
|
5
|
1/3
|
1
|
|
| Table 2 |
Criteria in pairwise comparisons |
Using verbal scales in pairwise comparisons has the advantage of allowing you to assign numerical values to elements that would otherwise appear to resist such comparisons. This makes the process of analyzing complex problems much easier because it gives you a common scale for both tangibles and intangibles. It also gives you the ability to trace value chains in hierarchies composed of many levels and elements. As you can see, the four criteria in the example are very different. The first two, cost and distance, are quantitative (tangible) criteria and relatively uncomplicated:
- With a budget limit of $20 per person, any more expensive restaurant is eliminated as a choice.
- Any prospective restaurant must be within a five-mile radius of the office; otherwise, you would lose too much time in travel.
The other two criteria are more intangible:
- You must choose a type of cuisine that will please all team members.
- The restaurant must have an atmosphere that is both pleasant and conducive to holding discussions.
After making pairwise comparisons and using the AHP software to make the necessary calculations, you assign each element in this matrix to its comparative value so that each criterion receives its appropriate relative weight in the decision hierarchy (Figure 3). In other words, the pairwise comparisons tabulated in Table 2 have been converted into the relative numerical values.
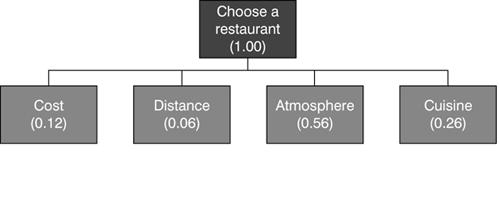
Figure 3
Criteria in the decision hierarchy with calculated values
Compare the Various Alternatives
You can further decompose any criterion into sub-criteria, sub-sub-criteria, and so on, as needed. You may want to determine, for example, what kinds of cuisine your team members prefer. After soliciting their preferences (using the same pairwise process as above), you may end up with a sub-hierarchy for the cuisine criterion, such as the one shown in Figure 4. This holds true for the atmosphere criterion as well: If you need to define more precisely just what this criterion entails, you define sub-criteria to do so.
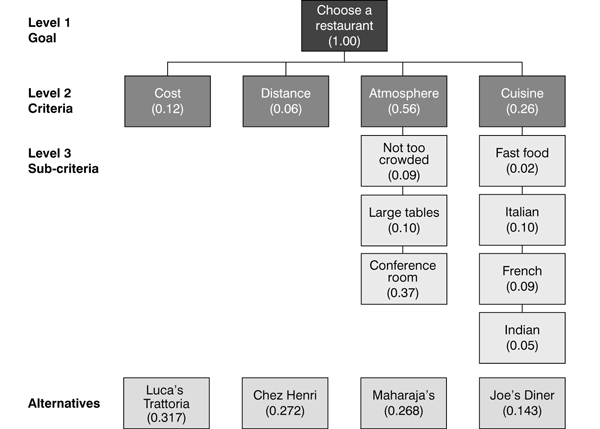
Figure 4
Completed hierarchy with computed relative values
Once you have compared the criteria and derived the weights of all of the elements on each level, you compute composite weights by aggregating the weights throughout the entire hierarchy. Finally, AHP compares the various alternatives to each other with respect to each of the criteria and sub-criteria and determines their relative weights. These weights form the basis for ranking the various alternatives. The best candidate to meet the goal will have the alternative with the highest ranking.
Selecting a Project Manager
Now that you understand some of the basic concepts of AHP, let’s look at how to apply them in the real world of an SAP implementation by analyzing a typical new project problem: selecting a project manager. For this example, I drill down to show how AHP can help to clarify this complex process, and I introduce a few new concepts as well.
Note
The decision hierarchy proposed here is only an example, which you can easily change or adapt for your own purposes. The criteria set is not definitive but representative, just to illustrate the process.
Project success results from the work of many people, but the project manager has the greatest responsibility, so you must choose this person with special care. Choosing the proper candidate for project manager is one of the most important decisions in an SAP implementation. Typically, SAP projects have two project managers, one on the customer side and one on the SAP integrator or partner side (a vendor). The user and the vendor may see the decision problem differently.
Identify the Project Requirements
Let’s focus on the example of choosing the appropriate project manager from the customer side. The customer usually begins by trying to find the right person among its in-house employees or available interim managers. The decision process ought to begin, however, by identifying the requirements of the project — that is, the criteria that must be met for this particular project to be a success. On this basis, you can then define both the general and specific skills and competencies that the project manager needs. These requirements may differ depending on the project type (e.g., SAP ERP implementation, FI/CO functionalities implementation, system optimization).
Most SAP practitioners agree that in project management, technical skills are less important than leadership and interpersonal skills. You should consider this when preparing your criteria hierarchy. Figure 5 proposes a hierarchy for this decision problem. (If there are several decision makers, it’s advisable to use the Delphi method to define the criteria set [see the Key Concept above.])

Figure 5
Hierarchy for selecting the project manager
Determining Resource Availability
Among the criteria listed in the hierarchy for choosing a project manager, decision makers sometimes omit the prospective candidate’s availability for the project. Sometimes, a potential project manager is already involved in multiple ongoing projects. Assigning a new project to this person may, despite their high-level skills and experience, lead to overload and the consequent failure of the project. You should assign a project to a project manager only if he or she can take on the additional work. Remember, overloading a project manager may cost you considerable switchover time, which is the loss (person-hours per time period) in the project manager’s capacity that occurs when he or she switches back and forth among multiple projects.
If a given project has a high priority, management may decide to release the prospective manager from other current projects so that he or she can have the resource availability needed to take on the new project. Discontinuity in management is not desirable, but in some situations, the success of a strategic undertaking is much more important than that of other projects. The capacity of the project manager is one of the criteria in Figure 5. The proposed example of estimating the effective capacity of the project manager in a six-month horizon is shown in Table 3.
| Available working days |
21 total
|
126
|
| Non-project work (25%) |
5.25 non-project work
|
31.5
|
| Other projects/tasks |
6 for other tasks
|
36
|
| Resource availability |
9.75 available
|
58.5
|
|
| Table 3 |
Effective capacity of a project manager |
Decision Problem Analysis
Now, let’s look at the decision problem. Starting from the top of the hierarchy (the goal), compare the criteria on the second level, with respect to the goal, with one another. You can enter your judgments verbally (Table 1). Table 4 illustrates the judgments matrix for the second level of the hierarchy and the resulting priorities, which the AHPproject software tool evaluates (www.AHPproject.com) to get the consistency ratio (CR, as shown in the top left corner).
|
CR=0.07
|
Experience
|
Knowledge
|
Personal/interpersonal skills
|
Business skills
|
Resource capacity
|
| Experience |
1
|
3
|
2
|
1
|
1
|
| Knowledge |
1/3
|
1
|
1/5
|
1
|
1/3
|
|
Personal/interpersonal skills
|
1/2
|
5
|
1
|
1
|
1
|
|
Business skills
|
1
|
1
|
1
|
1
|
1
|
| Resource capacity |
1
|
3
|
1
|
1
|
1
|
|
| Table 4 |
Judgments matrix for the second level of the hierarchy |
The matrix has as many rows and columns as there are elements connected to the goal. The numbers represent the dominance of the element in the row heading over the element in the column heading. For example, the experience criterion is moderately more important than the knowledge criterion (value 3, according to the Saaty scale). Knowledge, therefore, is one-third as important as experience. The decision maker accords both business skills and resource capacity an equal value (value 1 on the Saaty scale).
As in the first example, at least five entries in this judgments matrix are “ones”; they represent the self-comparisons (i.e., experience to experience, knowledge to knowledge, etc.) on the matrix diagonal (highlighted in yellow). The entries under the diagonal are reciprocal by virtue of the inverted comparison. You need 10 comparisons for this matrix: In general, you need n (n - 1) / 2 comparisons, where n is the number of elements on a given level (in this case, 5 (5 – 1) / 2 = 10). Once you have finished comparing criteria, the AHP software automatically computes the CR. As discussed in the sidebar “The Consistency Ratio” below, the CR should be = 0.10. If it isn’t, you need to review and possibly revalue the criteria.
Currency Ratio
Ideally, pairwise comparisons are perfectly consistent. For example, if I like apples twice as much as I like pears and pears twice as much as peaches, then I like apples four times as much as peaches (and, reciprocally, I like peaches one-quarter as much as apples). That is, when your judgments are consistent, mathematical transitivity, the relationship between mathematical expressions (such as equality or inequality), is reliable (2 × 2 = 4).
However, complications can quickly set in: What if I like fresh peaches during the summer, apples for making pies, and pears for homemade wine? As alternatives, criteria, and conditions multiply — as they do in any complex decision process — the chances increase that due to the subjective element of verbal judgments, some degree of inconsistency will arise. Because perfect consistency rarely exists in the real world, you need to determine an acceptable level of inconsistency.
For this reason, AHP calculates a consistency ratio (CR) for each set of pairwise comparisons. (Again, the software performs all the mathematical background calculations.) Perfect consistency yields a CR of 0.00.
Pairwise Comparisons
You must also make pairwise comparisons for the sub-criteria on the third level. Table 5 shows the results.
|
Compare the Sub-Criteria (Level 3) of Experience (Level 2)
|
CR=0.00
|
SAP experience
|
Project management/Project Management Professional (PMP) certificate
|
|
SAP experience
|
1
|
1/3
|
|
Project management/PMP certificate
|
3
|
1
|
Compare the Sub-Criteria (Level 3) of Knowledge (Level 2)
|
CR=0.00
|
Business knowledge
|
SAP module knowledge
|
Education level
|
|
Business knowledge
|
1
|
3
|
5
|
|
SAP module knowledge
|
1/3
|
1
|
2
|
|
Education level
|
1/5
|
1/2
|
1
|
Compare the Sub-Criteria (Level 3) of Personal/Interpersonal Skills (Level 2)
|
CR=0.04
|
Communication
|
Creativity
|
Conflict management
|
Decision-making
|
Personal integrity
|
Leadership
|
|
Communication
|
1
|
5
|
5
|
1
|
1
|
1
|
|
Creativity
|
1/5
|
1
|
1/2
|
1/2
|
1/2
|
1/5
|
|
Conflict management
|
1/5
|
2
|
1
|
1/2
|
1
|
1/2
|
|
Decision-making
|
1
|
2
|
2
|
1
|
1
|
1
|
|
Personal integrity
|
1
|
2
|
1
|
1
|
1
|
1
|
|
Leadership
|
1
|
5
|
2
|
1
|
1
|
1
|
Compare the Sub-Criteria (Level 3) of Business Skills (Level 2)
|
CR=0.00
|
Customer concern
|
Profit/cost-consciousness
|
|
Customer concern
|
1
|
1/2
|
|
Profit/cost-consciousness
|
2
|
1
|
|
| Table 5 |
Pairwise comparisons for the sub-criteria |
Note that resource capacity (level 2) has no sub-criteria (level 3); therefore, it also has no judgments matrix.
Then, you compare the candidates with respect to each sub-criterion (level 3). Table 6 shows the results. For example, candidate Andy Black is strongly preferred over Sue White (value 5, according to the Saaty scale) from the point of view of the criterion of SAP experience (level 2).
|
|
SAP experience
|
|
CR=0.00
|
Andy Black
|
Sue White
|
Ted Rose
|
Joan Gray
|
|
Andy
Black
|
1
|
5
|
5
|
3
|
|
Sue
White
|
1/5
|
1
|
1
|
1/2
|
|
Ted
Rose
|
1/5
|
1
|
1
|
1/2
|
|
Joan
Gray
|
1/3
|
2
|
2
|
1
|
|
Project management experience
|
|
CR=0.06
|
Andy Black
|
Sue White
|
Ted Rose
|
Joan Gray
|
|
Andy
Black
|
1
|
1/3
|
1
|
5
|
|
Sue
White
|
3
|
1
|
3
|
4
|
|
Ted
Rose
|
1
|
1/3
|
1
|
3
|
|
Joan
Gray
|
1/5
|
1/4
|
1/3
|
1
|
|
Business knowledge
|
|
CR=0.01
|
Andy Black
|
Sue White
|
Ted Rose
|
Joan Gray
|
|
Andy
Black
|
1
|
1/5
|
1
|
1/3
|
|
Sue
White
|
5
|
1
|
3
|
1
|
|
Ted
Rose
|
1
|
1/3
|
1
|
1/3
|
|
Joan
Gray
|
3
|
1
|
3
|
1
|
|
SAP module knowledge
|
|
CR=0.02
|
Andy Black
|
Sue White
|
Ted Rose
|
Joan Gray
|
|
Andy
Black
|
1
|
5
|
5
|
2
|
|
Sue
White
|
1/5
|
1
|
1
|
1/5
|
|
Ted
Rose
|
1/5
|
1
|
1
|
1/3
|
|
Joan
Gray
|
1/2
|
5
|
3
|
1
|
|
Education level
|
|
CR=0.03
|
Andy Black
|
Sue White
|
Ted Rose
|
Joan Gray
|
|
Andy
Black
|
1
|
1/7
|
2
|
1
|
|
Sue
White
|
7
|
1
|
6
|
7
|
|
Ted
Rose
|
1/2
|
1/6
|
1
|
1
|
|
Joan
Gray
|
1
|
1/7
|
1
|
1
|
|
Communication
|
|
CR=0.02
|
Andy Black
|
Sue White
|
Ted Rose
|
Joan Gray
|
|
Andy
Black
|
1
|
3
|
4
|
3
|
|
Sue
White
|
1/3
|
1
|
2
|
2
|
|
Ted
Rose
|
1/4
|
1/2
|
1
|
1
|
|
Joan
Gray
|
1/3
|
1/2
|
1
|
1
|
|
Creativity
|
|
CR=0.00
|
Andy Black
|
Sue White
|
Ted Rose
|
Joan Gray
|
|
Andy
Black
|
1
|
1/5
|
1
|
1
|
|
Sue
White
|
5
|
1
|
5
|
5
|
|
Ted
Rose
|
1
|
1/5
|
1
|
1
|
|
Joan
Gray
|
1
|
1/5
|
1
|
1
|
|
|
Conflict management
|
|
CR=0.01
|
Andy Black
|
Sue White
|
Ted Rose
|
Joan Gray
|
|
Andy
Black
|
1
|
6
|
5
|
6
|
|
Sue
White
|
1/6
|
1
|
1/2
|
1
|
|
Ted
Rose
|
1/5
|
2
|
1
|
2
|
|
Joan
Gray
|
1/6
|
1
|
1/2
|
1
|
|
Decision making
|
|
CR=0.07
|
Andy Black
|
Sue White
|
Ted Rose
|
Joan Gray
|
|
Andy
Black
|
1
|
2
|
4
|
1/2
|
|
Sue
White
|
1/2
|
1
|
2
|
1/2
|
|
Ted
Rose
|
1/4
|
1/2
|
1
|
1/2
|
|
Joan
Gray
|
2
|
2
|
2
|
1
|
|
Profit/cost-consciousness
|
|
CR=0.02
|
Andy Black
|
Sue White
|
Ted Rose
|
Joan Gray
|
|
Andy
Black
|
1
|
4
|
4
|
4
|
|
Sue
White
|
1/4
|
1
|
2
|
2
|
|
Ted
Rose
|
1/4
|
1/2
|
1
|
1
|
|
Joan
Gray
|
1/4
|
1/2
|
1
|
1
|
|
Personal integrity
|
|
CR=0.01
|
Andy Black
|
Sue White
|
Ted Rose
|
Joan Gray
|
|
Andy
Black
|
1
|
1
|
1
|
1/3
|
|
Sue
White
|
1
|
1
|
1
|
1/3
|
|
Ted
Rose
|
1
|
1
|
1
|
1/5
|
|
Joan
Gray
|
3
|
3
|
5
|
1
|
|
|
|
Leadership
|
|
CR=0.01
|
Andy Black
|
Sue White
|
Ted Rose
|
Joan Gray
|
|
Andy
Black
|
1
|
5
|
6
|
3
|
|
Sue
White
|
1/5
|
1
|
2
|
1/2
|
|
Ted
Rose
|
1/6
|
1/
|
1
|
1/3
|
|
Joan
Gray
|
1/3
|
2
|
3
|
1
|
|
Customer concern
|
|
CR=0.08
|
Andy Black
|
Sue White
|
Ted Rose
|
Joan Gray
|
|
Andy
Black
|
1
|
2
|
3
|
1/5
|
|
Sue
White
|
1/2
|
1
|
3
|
1/3
|
|
Ted
Rose
|
1/3
|
1/3
|
1
|
1/5
|
|
Joan
Gray
|
5
|
3
|
5
|
1
|
|
Resource capacity
|
|
CR=0.00
|
Andy Black
|
Sue White
|
Ted Rose
|
Joan Gray
|
|
Andy
Black
|
1
|
5
|
1
|
5
|
|
Sue
White
|
1/5
|
1
|
1/5
|
1
|
|
Ted
Rose
|
1
|
5
|
1
|
5
|
|
Joan
Gray
|
1/5
|
1
|
1/5
|
1
|
|
|
| Table 6 |
Judgment matrices for the alternatives (candidates) level in the hierarchy |
Overall Ranking Calculation
The final step in AHP is to get the overall ranking of the candidates (the program performs this calculation for you). The AHP method uses the judgment matrices to determine the final ranking. The result in Table 7 reveals that Andy Black is most likely the best candidate for the project manager position because he enjoys the highest (or heaviest) weighting.
|
Andy Black
|
0.376
|
|
Sue White
|
0.239
|
|
Ted Rose
|
0.196
|
|
Joan Gray
|
0.188
|
|
| Table 7 |
Overall weights of candidates |
The AHP software delivers many possible graphical presentations of the decision process results. Figure 6 and Figure 7 graphically represent example overall weights for alternatives and criteria. These can be helpful when you are making the case for a particular decision.
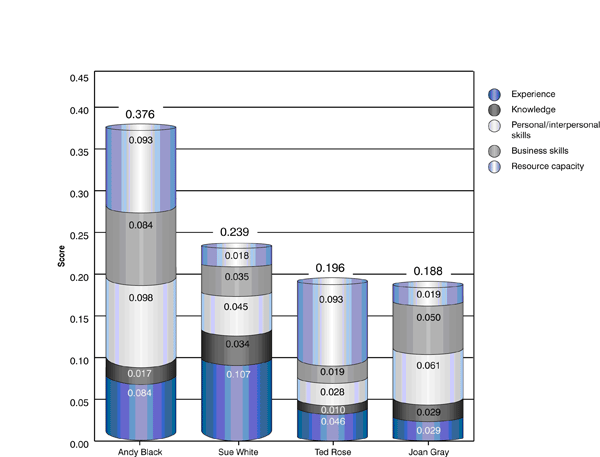
Figure 6
Candidate rankings with weights and shared criteria
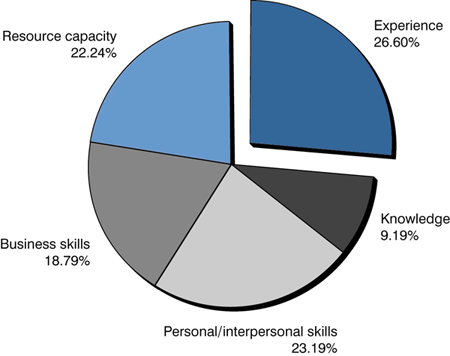
Figure 7
Criteria weights
Figure 8 is a spider (or radar) diagram that compares the final priorities of the two candidates with the best scores, Andy Black and Sue White. The chart shows that Andy Black is definitely the better candidate from the perspectives of resource capacity, business skills, and personal/interpersonal skills. Such diagrams are useful visual tools that can help you to determine the differences between the alternatives you are comparing.
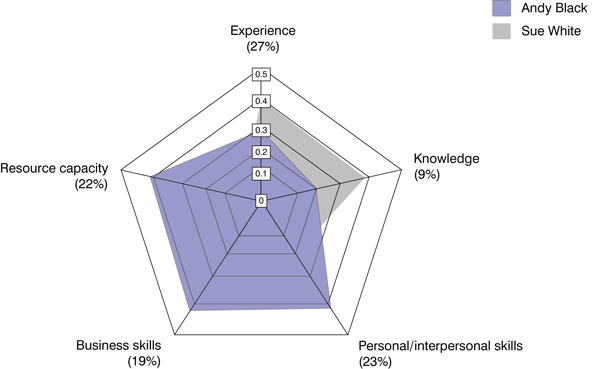
Figure 8
Evaluation of top two candidates on a spider diagram
It’s good practice to analyze the sensitivity of the decision problem solution (see the sidebar “Sensitivity Analysis of Criteria Change” below). Typically, you do this for the chosen criteria. For example, Figure 9 shows that the final ranking would change if the candidates’ resource capacity criterion had a relative weight of value 0.35 (instead of the current value of 0.22). In that case, Sue White would be a worse candidate than Ted Rose.
Sensitivity Analysis of Criteria Change
Usually, the decision maker wants to make sure that the ranking he or she gets is robust with regard to variations in the criteria weights. In real-world problems, complete information to help you compare criteria isn’t typically available. A sensitivity analysis shows how the final ranking changes when the decision maker’s preferences for criteria change. If small changes (e.g., 5%) in criteria weights don’t affect the result of the analysis, the ranking is stable and satisfactory. If small changes do affect the analysis, the decision maker should be aware of it and seek additional information. The classical one-dimensional sensitivity analysis tells you whether the final outcome will remain stable even if the criteria weights vary by a few percentage points.
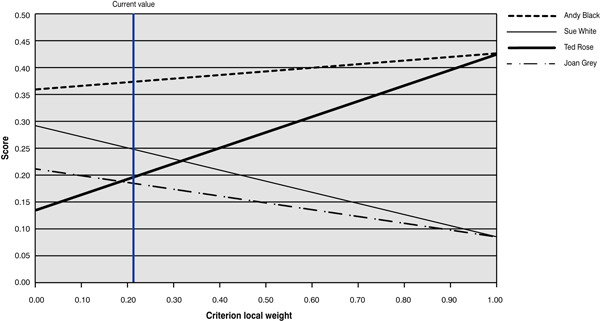
Figure 9
Sensitivity analysis for the resource capacity criterion
According to Figure 10, if the weight of the personal/interpersonal skills criterion changed from 0.2319 to 0.3000, Joan Gray would be preferable to Ted Rose. When you analyze all of the criteria in that way, the score of the best candidate, Andy Black, has a strong basis (meaning that changing the criteria weights across a wide range would not influence the first position in the ranking), while the other candidates’ ranking positions are weaker (small changes in criteria weights may change their ranking). Therefore, the decision maker can conclude that his or her choice of the best candidate for the project manager position, Andy Black, is based on a strong and objective foundation.
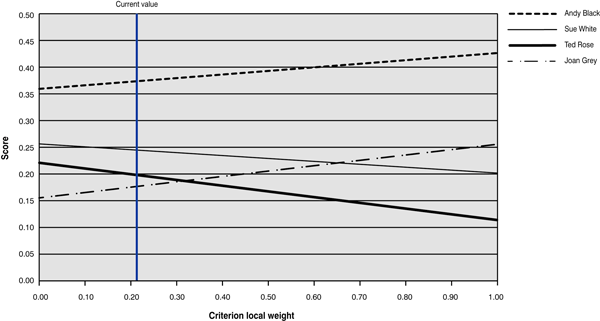
Figure 10
Sensitivity analysis for the personal/interpersonal skills criterion
Additional Decision Problems
Now, you can see how to use the AHP method to resolve a decision problem. The main difficulty is how to structure a good problem hierarchy. Next, I propose several sample hierarchies for typical SAP implementation problems that you can adjust to your own requirements.
Time-Compression Scenario Selection
One of SAP project managers’ main tasks is monitoring the project schedule. The critical-path project activities are of crucial importance for the schedule. The critical path is that part of the project that cannot tolerate any delays. The critical path has no float (i.e., no slack time), the amount of time you can delay the start of the project task without affecting the planned finish date, so you must carefully manage the tasks on the critical path. If even one of these tasks slips, the end date of the project can slip as well. From another perspective, the tasks on the critical path can also potentially shorten the duration of a project.
Changes in customer requirements, legal requirements, and contractor schedules may lead to revising the project plan. New completion dates may be unacceptable to the project stakeholders, so the project manager needs to find an effective way to accelerate project completion. If you have delays on the critical path, the project manager may use one of two techniques: crashing (a project schedule compression technique in which you add more resources to the activities that lie on the critical path to shorten project duration) or fast tracking (a project schedule compression technique in which you change activity relationships; activities that you might originally have performed in sequence are changed to perform in parallel).
With the crashing technique, the project manager analyzes the critical path and determines what can be done to shorten it. The project manager must analyze cost and schedule tradeoffs as well. Crashing may result in a shorter schedule, but it can also push the project’s budget beyond the acceptable range. To balance the potential tradeoffs and still reduce the length of a project’s critical path, the project manager needs to look for opportunities to change or modify the activity-sequencing, increase the number of team members, or improve the technology. Each opportunity brings some risks; for example:
- Changing the activity sequence often contradicts best practices (e.g., beginning an SAP configuration before you close the SAP Business Blueprint phase is risky because subsequent changes to the blueprint may require reconfiguration).
- Increasing the number of team members increases your communication requirements and training efforts.
With the fast-tracking technique, the project manager looks for opportunities to complete critical-path activities in parallel rather than in sequence. Fast tracking can raise risks and costs beyond an acceptable threshold and often results in redoing work, nullifying the time saved.
Of the two techniques, crashing is preferable. AHP can help you resolve the decision problem of whether a crashing or fast-tracking scheme is better in a given situation. Most people consider only time and cost when choosing the time-compression scheme. However, you should also consider other criteria, such as project quality and team morale. Figure 11 presents the proposed decision hierarchy for this example.
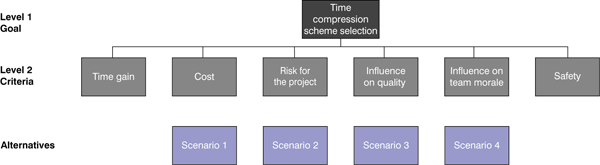
Figure 11
Hierarchy for selecting a time-compression scheme
Note
Aggregating cost criteria with benefits in a single hierarchy assumes that the decision maker wants to answer the question: “With respect to the goal, what is the relative value between benefits and costs?” Sometimes, you might use two separate hierarchies to analyze benefit and cost criteria and then calculate a benefit/cost ratio. In this case, the alternative with the highest ratio is the best solution. This approach assumes that you measure both benefit and cost priorities in the same commensurate units. However, that’s not usually the case, so the direct integration of benefits and costs into a single hierarchy is a better approach.
Project Scope Management
I have never seen a completed SAP project that had no unforeseen changes to its scope. You usually define the project scope early in the planning phase, so many reasons crop up to change it later: New internal requirements, changing legal requirements, and fluctuating external market conditions may alter the nature of the project as it progresses. An experienced project manager should give top priority to scope management because scope changes generate additional costs and schedule changes. This may affect the project’s critical path, and team morale will fluctuate accordingly (more unplanned work equals less motivation). Even though they are very large, SAP projects still tend to have limited budgets; therefore, not all of the proposed changes are likely to be approved. How do you decide which changes to approve and which to reject? You can find the answer by ranking the changes and approving those with the highest scores until the scope falls within the budget limits. Figure 12 presents a proposed problem hierarchy for project scope changes.
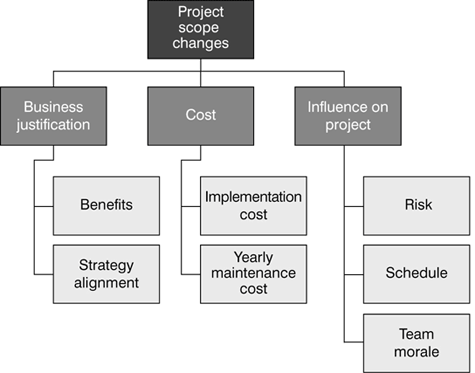
Figure 12
Hierarchy for selecting changes in project scope
Tip!
New reporting requirements frequently necessitate changes in scope that you didn’t initially plan. If the list of new reports (e.g., to be prepared in ABAP or Business Server Pages [BSP]) is long and the budget for enhancements is limited, AHP may help you to rank them, select the most important ones, and reject those of low priority.
Project Portfolio Management
Several constraints limit the planning of new projects, the strictest one being the budget. Let’s assume that a sample company with an SAP system is preparing its SAP projects budget for the coming year. Because of limited finances, the budget covers only the best proposals, so the decision maker must choose from the following:
- Upgrade your SAP system
- Implement SAP Enterprise Compensation Management
- Employ SAP E-Recruiting
- Implement SAP Cost and Quotation Management
- Optimize your processes
This is a typical decision problem, and AHP seems to be the perfect tool to solve it. Figure 13 shows a sample decision tree.
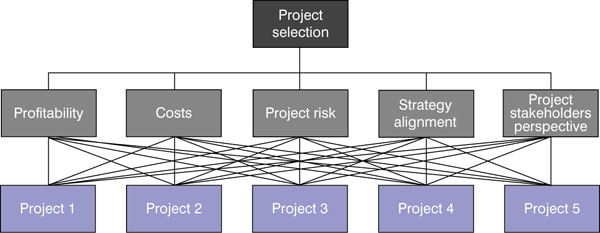
Figure 13
Decision tree for selecting the most important projects
Note
Your decision tree for project selection may be more complex and have more levels than this. You can split the profitability criterion into several financial metrics, such as return on investment (ROI), net present value (NPV), and internal rate of return (IRR).
The Project Stakeholders Perspective criterion (on the right) generalizes several criteria related to various groups of project addressees. For example, the expectations of members of the board may have greater weight than the expectations of specialists in one of the company’s departments.
Figure 14 presents sample rankings for the portfolio after AHP comparisons. These results make it much easier for decision makers to choose projects for next year’s plan.
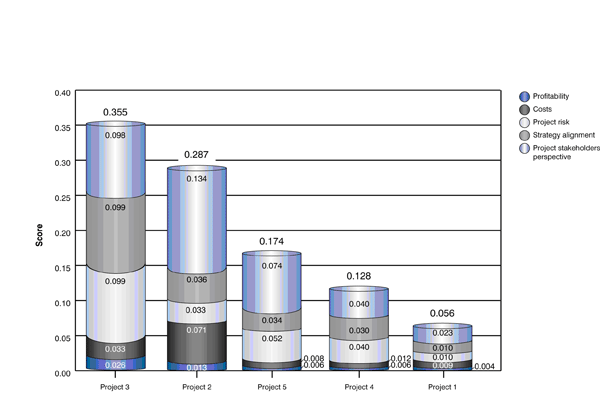
Figure 14
Ranking of projects with weights and shared criteria
AHP can be helpful in a situation when all projects from the portfolio are in progress, but due to budget trimming, it’s necessary to suspend or withdraw from some undertakings. The ranking of projects clearly indicates their importance to the organization and thus facilitates making impartial and objective decisions.
References
- Duplaga, E.A., and M. Astani (2003), “Implementing ERP in manufacturing,” Information Systems Management, 20(3).
- Fallon, M. (2005), “Enterprise resource planning implementation through the use of change management and critical success factors,” (https://www.comp.dit.ie/rfitzpatrick/MSc_Publications/2005_Maurice_Fallon.pdf), retrieved July 22, 2006.
- Forman, E. and M. Selly, “Decision by Objectives,” Developing a Decision Hierarchy (https://mdm.gwu.edu/forman/DBO.pdf).
- Saaty, T.L., Decision-making for Leaders: The Analytic Hierarchy Process for Decisions in a Complex World (RWS Publications, 2008).
- Saaty, T.L., The Analytic Hierarchy Process: Planning, priority setting, resource allocation (McGraw-Hill, 1980).
- Stratman, J.K., and A.V. Roth (2002). “Enterprise Resource Planning (ERP) competence constructs: Two-stage multi-item scale development and validation,” Decision Sciences, 33(4).
Michael Szardenings
Michael Szardenings is a senior developer in the SAP IMS organization. Working in the Systems Management Group within IMS, Michael is responsible for all kinds of Windows printing from SAP systems. He started his career in 1989 in the IBM Research and Development Lab in Germany, with the development of various user interface components for IBM mainframe computers. As SAP IBM came together on several joint venture projects in the systems management area, which includes job scheduling and printing, Michael’s focuses switched to SAP. He joined SAP in 2001.
You may contact the author at editor@sappro.com.
If you have comments about this article or publication, or would like to submit an article idea, please contact the editor.



















